Las parábolas aparecen en diferentes situaciones de la vida cotidiana. Se puede apreciar claramente cuando lanzamos un balón bombeado o golpeamos una pelota de tenis. En la curva que describe la pelota en su movimiento se puede ver que se trata de una trayectoria parabólica. Al dibujar este desplazamiento, podemos considerar esta parábola como la representación gráfica de una función que asigna a cada desplazamiento horizontal ‘x’ la altura ‘y’ alcanzada por la pelota.
Una vez situada la parábola en este marco, que es un sistema de coordenadas cartesianas, son visibles dos propiedades fundamentales: tiene un punto extremo, que corresponde al instante en el que la pelota alcanza la altura máxima. Este punto es el vértice de la parábola; y la segunda, en la que las alturas a las que llega la pelota son las mismas en posiciones horizontales equidistantes de la abcisa del vértice. Por tanto, la recta paralela al eje de ordenadas que pasa por el vértice es el eje de simetría de la parábola.


Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.
La distancia entre el foco y la directriz de una parábola, recibe el nombre de parámetro de la parábola (suele denotarse por p).
Dada una parábola, se llama eje de simetría, la recta que contiene al foco y es perpendicular a la directriz.
Si la curva de la parábola, debe cortar en el eje x en el punto cero.
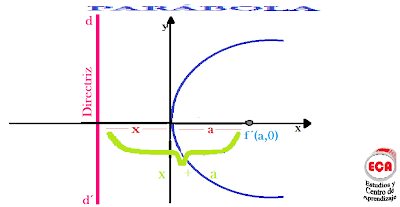
Sean d d´ la directriz y f el foco, la recta y el punto fijo. Tracemos por
f (a,0), la perpendicular al eje x.
Sea 2 a la distancia de f a DD´.
Por definición de parábola la curva debe cortar el eje x en el punto 0, equidistante de f y DD´. El eje y, se traza perpendicular al x por el punto 0.
Las coordenadas de f son (a,0)
La ecuación de la directriz es: x + a = 0 o bien
x = - a.
x = - a.
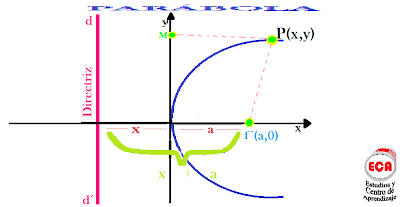
Sea P(x, y), un punto genérico cualquiera.
Sea P(x,y) un punto genérico cualquiera de manera que
Entonces:
De la forma de la ecuación:
, se deduce que la parábola es simétrica con respecto al eje x.
El punto en que la curva corta el eje de simetría se denomina Vértice.
La cuerda CC´que pasa por el foco y es perpendicular al eje se llama latus rectum.
La longitud del latus rectum es 4a, es decir el coeficiente del término de primer grado en la ecuación.
Si el foco está a la izquierda de la directriz, la ecuación toma la forma:
Si el foco pertenece al eje y, la forma de la ecuación es:
En la que el signo depende de que el foco esté por encima o por debajo de la directriz.
Consideremos ahora una parábola de vértice el punto P (h,k), de eje paralelo al de coordenadas x y cuyo foco esté a una distancia a del vértice y a la derecha de él. La directriz. Paralela al eje y y a una distancia 2ª a la izquierda del foco, tendrá la ecuación x = h – a o bien, x – h + a = 0.
Llamaremos P(x, y) un punto genérico cualquiera de la parábola. Como PF = PM
Se llama vértice de la parábola al punto que corta su eje.
Para simplificar la parábola, se supondrá que el vértice es el origen de las coordenadas P (0,0) y que el foco (f), se encuentra en el semieje positivo de las abscisas.
FUNCION CUADRATICA.
Definición.
Una función cuadrática es aquella que puede escribirse de la forma: f(x) = ax2 + bx + c, donde x es la variable independiente; y es la variable dependiente; a, b y c coeficientes de la función y estos son números reales cualesquiera y a distinto de cero. Si representamos "todos" los puntos (x, f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.
La gráfica de la función cuadrática es una parábola y puede tener una de las siguientes seis posiciones.
Es decir, se puede abrir hacia arriba (figuras 1,2 y 3) o hacia abajo (figuras4, 5 y 6) y puede interceptar al eje x en dos puntos (figura 1 y 4), en un punto (figuras 2 y 5) o ningún punto (figuras 5 y 6)
A continuación se muestran tres funciones cuadráticas con sus respectivas gráficas, de tres funciones cuadráticas muy sencillas:
Para determinar el valor de las soluciones X1 y X2 respectivamente es necesario utilizar la siguiente formula:
Los valores correspondientes a, a, b y c, los desprendemos de la ecuación general de la forma: a x2 + bx + c = 0
La concavidad de la parábola
O la posición en que se abre (hacia arriba o hacia abajo) está determinada por el signo del coeficiente de x2
En la función y = a x2 + bx + c, es decir, está determinada por el signo de “a”.
Así:
· Si a > 0, entonces la concavidad es positiva y la parábola se abre hacia arriba.
· Si a < 0, entonces la concavidad es negativa y la parábola se abre hacia abajo.
Nota: “a” no puede tomar el valor cero, pues entonces la función sería lineal y no cuadrática.
Intersección de la parábola con los ejes.
a)-.Intersección con el eje Y: Como todos los puntos de este eje tienen la abscisa (eje x) x = 0, el punto de corte de la parábola con el eje Y tendrá de coordenadas (0, y).
La intersección de la parábola con el eje y se obtiene haciendo x = 0 y corresponde por supuesto a y c.
Todas las parábolas tienen un vértice, que corresponde al valor mínimo (si la parábola se abre hacia arriba). O el valor máximo (si se abre hacia abajo).
b)-. Intersección con el eje X: Como todos los puntos del eje X tienen la ordenada (eje y) y = 0, para ver estos puntos de corte se resuelve la ecuación de segundo grado ax2 + bx + c = 0.
Las intersecciones de la gráfica con el eje x, corresponden a las soluciones de la ecuación cuadrática asociada, es decir, a:
ax2 + bx + c = 0 (Cuando y toma el valor de cero, la gráfica está sobre el eje x)
Como sabemos, los tipos de soluciones de la ecuación dependen del signo del discriminante ∆ = b² - 4ac.
· Si ∆ = b² - 4ac → ∆ > 0, entonces las soluciones son reales y distintas y por lo tanto, hay 2 intersecciones con el eje x, éstas son los puntos X1 y X2.
· Si ∆ = b² - 4ac → ∆ = 0, entonces las soluciones son reales e iguales y por lo tanto, hay una sola intersección con el eje x, aquí X1 = X2.
· Si ∆ = b² - 4ac → ∆ < 0, entonces las soluciones son complejas conjugadas, y por lo tanto, no hay una intersección con el eje x.
Dependiendo del valor del discriminante (D) de la ecuación, se pueden presentar tres situaciones distintas:
A-.Si D > 0, la ecuación tiene dos soluciones reales sean X1 y X2 y estas sean distintas y la parábola cortará al eje X en dos puntos.
B-.Si D = 0, la ecuación tiene una solución real es decir X1 = X2 y, por tanto, la parábola cortará al eje X en un punto (que será el vértice).
C-.Si D < 0, la ecuación no tiene soluciones reales y la parábola no cortará al eje X.
EJERCICIO RESUELTO PASO A PASO
1.
EJERCICIO RESUELTO PASO A PASO
1.

































No hay comentarios:
Publicar un comentario
TU COMENTARIO O SUGERENCIA NOS HARÁ CRECER