VARIABLES DE UNA FUNCIÓN

·         UNA VARIABLE

·         FUNCIÓN DE UNA VARIABLE

·         VARIABLES INDEPENDIENTES Y DEPENDIENTES.

·         LA NOTACIÓN FUNCIONAL

·         SISTEMA DE COORDENADAS RECTANGULARES

·         GRÁFICOS ESTADÍSTICOS 

·         EJERCICIOS RESUELTOS

UNA VARIABLE es un símbolo al que se le puede asignar un conjunto de valores. Una constante es un símbolo al que solo se le puede asignar un valor.

            Para representar las variables se emplean las letras finales del alfabeto x, y, z, u, v, w,  y para las constantes se emplean las primeras, a, b, c.

FUNCIÓN DE UNA VARIABLE. Una variable y es función de otra x si existe una relación entre ambas, x e y, de forma que cada valor de x le corresponda uno, o más de y. En este capítulo, sólo consideramos números y funciones reales.

Ejemplo 1:

Y = x² - 5x + 2 establece una relación entre las variables x e y. Cuando x toma los valores x= 0, 1, 2, -1, los correspondientes de y son: 8,  2, - 2,  - 4

Ejemplo 2:

La longitud C de la circunferencia es una función del radio r  dada por la expresión  C= 2πr. Las longitudes de las circunferencias de radios 1, 3, 5 (metros) son, respectivamente: 2π, 6π, 10π (metros).

Ejemplo 3:

La población y de una nación es función del año x. En el cuadro siguiente representa la población de los Estados Unidos con intervalos de diez años entre  1880 -  1950.

Cuando a cada valor de x le corresponde un solo valor de y, se dice que y es una función uniforme de x; en caso contrario, y es una función multiforme de x.

Por consiguiente, en los Ejemplos 1 y 3 anteriores, y es una función uniforme de x, ya que a cada valor de x le corresponde uno, y sólo uno, de y. Análogamente, en el ejemplo 2. C es una función uniforme de r.

Sin embargo, y = ± √x

Es una función multiforme de x, ya que cada valor cada valor de x le corresponden dos valores de y (excepto para solución trivial x = 0). Por ejemplo, si x= 4, y es ± 2  si x= 5, y = ± √5  etc.

VARIABLES INDEPENDIENTES Y DEPENDIENTES. La variable  a  la que se asignan valores (x en los ejemplos anteriores) se denomina variable independiente; la variable cuyo valor viene determinado por el que toma (y en los ejemplos) se llama variable dependiente o función. Decir que y es función de x equivale a decir que y depende de x.

El conjunto de valores que puede tomar la variable independiente recibe el nombre de campo de variación de la variable.

Ejemplo 1:

Y = x² - 5x + 2, x puede ser cualquier número real.

Ejemplo 2:

 C= 2πr, la variable independiente es el radio r de la circunferencia. El campo de variación de r es el conjunto de todos los números positivos y el cero.

Ejemplo 3:

La población y de una nación es función del año x. El campo de variación de x está formado por los años 1880,…..1950.

La variable independiente x es el conjunto de los números reales mayores o igual a cero, lo cual se representa por x ≥ 0.

Ejemplo 4:

            En la función y = ± √x, si se quiere que y siempre real, los valores que se pueden asignar a la variable independiente x es el conjunto de todos los números mayores o igual a cero, lo cual se representa por x ≥ 0.

Ejemplo 5:

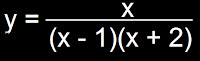            En la función  la variable x puede tomar cualquier valor real excepto x = 1 y x = - 2, para los cuales la función y no está definida. Por consiguiente, el campo de variación está constituido por el conjunto de los números reales excepto 1 y – 2.

EJERCICIOS RESUELTOS

LA NOTACIÓN FUNCIONAL y = f (x), que se lee “y igual a f de x”, es la que se utiliza para representar que y es una función de x, Según esta notación, f(a) significa el valor de la variable dependiente y cuando x = a (siempre que dicho valor exista).

            Así, pues, y = x² - 5x + 2 se puede escribir f(x) = x² - 5x + 2.

Por tanto, f (2), que es el valor de f(x) o cuando x = 2, x = - 1 es:

y = x² - 5x + 2

x = 2  y = (2)² - 5(2) + 2 = -4

x = -1 y = (-1)² - 5(-1) + 2 = 8

            En la notación funcional se puede emplear una letra cualquiera; esto es, g(x), h(x), F(x), etc, representan, asimismo, funciones de x.

SISTEMA DE COORDENADAS RECTANGULARES. Se utiliza para representar, gráficamente, una relación entre dos variables.

Sean X  -X e Y   -Y dos rectas  perpendiculares entre sí que se cortan en el punto 0-

La recta X – X, denominada eje x, se sitúa normalmente en posición horizontal.

La recta Y   -Y, se denomina eje y, se sitúa normalmente en posición vertical.

El punto o recibe el nombre de origen del sistema.

Empleando una unidad de longitud adecuada se pueden situar sobre el eje x, a la derecha e izquierda del origen 0, los puntos 1, 2, 3, 4,…. y -1, -2, -3, -4, -5,…., sin más que ir tomando, sucesivamente, dicha unidad de longitud.

            Los ejes x e y dividen al plano en 4 regiones o cuadrantes, denominados I, II, II, IV.

            Sea P un punto cualquiera del plano xy. Trazando desde P las perpendiculares a los ejes x e y, los valores de x e y de los puntos de intersección de dichas perpendiculares con los ejes determinan, respectivamente, la coordenada x (abscisa) y la coordenada y (ordenada) del punto P. Estas coordenadas se representan por el símbolo (x, y).

Recíprocamente, dadas las coordenadas de un punto, se puede situar éste en el plano x y.

Por ejemplo, las coordenadas de un punto P, de la figura son (3,2). El punto cuyas coordenadas son (-2, -3) es Q.

GRÁFICA DE UNA FUNCIÓN y = f(x) es el lugar geométrico de los puntos (x,y) que satisfacen a la ecuación y = f(x).

FUNCIÓN DE DOS VARIABLES. Se dice que una variable z es función de las variables x e y si existe una relación tal que a cada par de valores de x e y le corresponde uno o más, valores de z. En este caso, x e y son variables independientes, y z es la variable dependiente o función.

            La notación funcional que se utiliza es z = f(x, y), que se lee “z igual a f de x”. Entonces, f(a, b) representa el valor de z cuando x = a e y = b, siempre que la función esté definida para dichos valores.

            Por ejemplo, si:

F (x, y) = x³ + xy² - 2x; x = 2 y y = 3

F (2, 3) = 2³ + (2) (3)² - 2(3)

F (2, 3) = 8 + 18 – 6

F (2, 3) = 20

            De igual forma se definirían las funciones de más de dos variables.

GRÁFICOS ESTADÍSTICOS  Son aquellos que representan una relación entre dos datos obtenidos de observaciones efectuadas en experimentos científicos, censos, operaciones comerciales, etc.

EJERCICIOS RESUELTOS