UN RECIENTE ESTUDIO REVELA QUE LA EVOLUCIÓN DE LOS RIBOSOMAS, LAS MOLÉCULAS MÁS ANTIGUA EN LOS SERES VIVOS, PUEDE OFRECER LA CLAVE DEL ORIGEN DE LA VIDA

En la foto son los ribosomas 
de la glándula salival de un
 insecto. Los ribosomas son las superestructuras
 biológicos que traducen la 
información genética en las

pequeñas fábricas biosintéticas 

proteins.These convertir la
 información genética del ADN
 en una
 secuencia de aminoácidos - que 
es la estructura primaria de
 las proteínas que componen 
nuestro cuerpo.
Según los datos del estudio “Daily Mail”, la evolución de los ribosomas, unas moléculas de 4.000 millones de años, puede explicar cómo las primeras moléculas de la vida en la Tierra primitiva formaron los propursores de las proteínas modernas y el ARN.

Los investigadores indican que el núcleo del ribosoma es esencialmente el mismo en todos los seres vivos, pero su capa exterior se expande a medida que el organismo evoluciona y se hace más complejo. Mediante la descamación digital de las capas de ribosomas modernos los expertos lograron modelar la estructura de los ribosomas primordiales.

"La historia de los ribosomas nos habla del origen de la vida", dice Loren Williams, profesor de la Facultad de Química y Bioquímica del GIT. "En su esencia, el ribosoma es el mismo en todas partes. El ribosoma es la biología universal".

Evolución del "sistema operativo" de la vida reveló: moléculas de 4 mil millones de años de edad, podrían proporcionar pistas a los orígenes de la existencia.

¿QUÉ ES UN RIBOSOMA?

Los ribosomas son las superestructuras biológicos que traducen la información genética en proteínas.

Estas pequeñas fábricas biosintéticas converte la información genética del ADN en una secuencia de aminoácidos - que es la estructura primaria de las proteínas que componen nuestro cuerpo.

En cada célula viva, la información contenida en el núcleo de una célula es 'transferido' de un ARN mensajero (ARNm).

El ARNm sale del núcleo y viaja a algo conocido como el retículo endoplasmático, donde dos subunidades del ribosoma se reúnen alrededor de ella y comienzan a sintetizar proteínas.

Cientos de miles de ribosomas funcionan en cada célula viva.

Por ejemplo, las células se replican rápidamente, tales como las células del hígado, pueden contener unos pocos millones de ribosomas.Incluso las células bacterianas pueden contener hasta 100.000 ribosomas.

En un nuevo estudio, los científicos compararon las estructuras tridimensionales de los ribosomas de una variedad de especies de diversa complejidad biológica, incluidos los seres humanos, levaduras, bacterias y arqueas. Los investigadores encontraron huellas distintas en los ribosomas que se han añadido nuevas estructuras a su superficie

Los ribosomas contienen secretos sobre cómo se reunieron las primeras moléculas de la vida.

1.- Son fábricas de una célula, la traducción de la información genética en proteínas.

2.- Los científicos en Atlanta peladas digitalmente vuelta capas de ribosomas modernos.

3.- Estudio encontró corazón de un ribosoma humana es la misma que en un ribosoma molde.

4.- Llegó a la conclusión de que la evolución puede añadir cosas al ribosoma, pero no puede cambiar lo que ya estaba allí.

Todos los seres vivos en la Tierra depende de una maraña misteriosa de moléculas llamadas ribosomas.

Estos son fábricas de proteínas de la célula, la traducción de la información genética en el ADN en una secuencia de aminoácidos para crear proteínas.

Los científicos creen que el ribosoma - cuya historia es una pista difícil - contiene pistas sobre cómo las primeras moléculas de la vida llegó hace en conjunto en torno a cuatro millones de años.

un nuevo estudio, los científicos compararon las estructuras tridimensionales de los ribosomas de una variedad de especies de diversa complejidad biológica, incluidos los seres humanos, levaduras, bacterias y arqueas.

Los investigadores encontraron huellas distintas en los ribosomas que se han añadido nuevas estructuras a su superficie.

Ahora los investigadores están un paso más cerca de descubrir estas pistas después de modelar la evolución de estas fábricas biológicas en un detalle sin precedentes.

núcleo del ribosoma es esencialmente el mismo en todos los sistemas vivos, mientras que las regiones externas se expanden y se vuelven complicado como especies ganan complejidad.

Por digitalmente pelar las capas de los ribosomas modernas, los científicos del Instituto de Tecnología de Georgia en Atlanta fueron capaces de modelar las estructuras de la primera de estas fábricas biológicas.

'La historia del ribosoma nos habla del origen de la vida ", dijo Loren Williams, profesor en la Facultad de Química y Bioquímica en el Instituto de Tecnología de Georgia.

"Hemos trabajado en un buen nivel de detalle cómo se originó y evolucionó el ribosoma.

Los seres humanos tienen los ribosomas más grandes y complejos.

'Pero los cambios están en la superficie - investigadores encontraron el corazón de un ribosoma humana es la misma que en un ribosoma molde.

Origins and ovolution of the first forms of ARN

Cientos de miles de ribosomas funcionan en cada célula viva. Por ejemplo, las células se replican rápidamente, tales como las células del hígado, pueden contener unos pocos millones de ribosomas. Incluso las células bacterianas pueden contener hasta 100.000 ribosomas. Ribosoma (en la foto) se puede encontrar en diferentes partes de una célula

mmmmmmmmmmmmmmmmmmm

LÍMITE DE UNA FUNCIÓN - Definición formal

Definición formal de límite que usa epsilon y delta enunciada por primera vez por el matemático cauchy. La definición nos dice:

El límite de una función es L si y sólo si para todo épsilon mayor que cero existe un delta mayor que cero tal que el valor absoluto de la función menos el límite es menor que épsilon siemmmpre que el valor absoluto de x menos a ( donde a es el valor al que tiende la x) sea menor que delta pero mayor a cero. 

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

Definición formal de límite que usa epsilon y delta enunciada por primera vez por el matemático cauchy. La definición nos dice:

El límite de una función es L si y sólo si para todo épsilon mayor que cero existe un delta mayor que cero tal que el valor absoluto de la función menos el límite es menor que épsilo n siempre que el valor absoluto de x menos a ( donde a es el valor al que tiende la x) sea menor que delta pero mayor a cero. 

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

Definición formal de límite que usa epsilon y delta enunciada por primera vez por el matemático cauchy. La definición nos dice:

El límite de una función es L si y sólo si para todo épsilon mayor que cero existe un delta mayor que cero tal que el valor absoluto de la función menos el límite es menor que épsilon siempre que el valor absoluto de x menos a ( donde a es el valor al que tiende la x) sea menor que delta pero mayor a cero. 

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

LÍMITES DE UNA FUNCIÓN - Cómo encontrar el límite de una función de variable real   

SOLUCIÓN DE LÍMITES apoyados en el hecho de que  siempre y cuando a sea parte del dominio de la función.

Nuestro primer ejemplo es: 

Si evaluamos directamente esta función:



Nos encontramos con 0/0, porque 4 no forma parte del dominio de la función. Recordemos que el dominio de de las funciones racionales son todos los números reales excepto los números que anulan el denominador. 

Dijimos que 0/0, existe una esperanza que, a través de factorización, podemos eliminar una indeterminación de la forma cero dividido cero y encontrar el límite.

El segundo ejemplo es:

Si la evaluamos directamente, obtenemos:

Cuando se presenta un  caso, donde el numerador es un número y el denominador es un cero; puede ocurrir dos cosas, podría ocurrir que el límite definitivamente no existiera o que el límite exista y sea infinito. 

Aquí sabemos que el límite es un infinito, lo que nos corresponde es saber si el límite existe o no, y si existe, saber si el infinito es 

Se recomienda usar la tabla numérica que ayudará a determinar el signo del infinito.

basados en el hecho de que para que exista el límite de una función al acercarnos por la izquierda y derecha debemos obtener el mismo resultado.

 Vemos que, usando tablas de signos,  el límite cuando nos acercamos a la función desde la izquierda es +∞ y cuando nos acercamos a la función desde la derecha es -∞, por lo tanto decimos: 

Concluimos el caso, donde el límite no existe. 

Algo  más  complejo dentro del cálculo de límites, es por ejemplo: Esta función racional.

donde el 2 no forma parte del dominio, porque se forma un cero en el denominador.

Con 0/0 no podemos decrir si el límite existe o no, sospechamos que es un infinito, pero aún no podemos llegar a esa conclusión.

Este tercer ejemplo nos muestra que para eliminar una indeterminación será a  través de racionalización. 

Aquí podemos evaluar diractamente, porque en x -> 2 no anula la función .

>mmmmmmmmmmmm

LÍMITES DE UNA FUNCIÓN - Álgebra o propiedades de un límite

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

Propiedad Distributiva

1.- Límite de la suma y resta de funciones.

2.- Límite del cociente y producto de funciones.

3.- Límite  de una función constante.

4.- Límite del producto una constante de una función.

5.-  Límite de una potencia

6.-  Límite de una raíz.

7.- Función exponencial o potencia de dos funciones.

Pero en este caso se hace con el fin de mostrar la propiedad más importante de todas, y es que el límite de una función en punto cualquiera "a" donde "a" hace parte del dominio de la función es precisamente el valor de la función evaluada en dicho punto, lo cual sirve para encontrar la gran mayoría de límites que se presentan en cálculo.

Lim x tiende a "a" de f(x) es igual a f(a) siempre que "a" pertenezca al dominio de f(x). 

 EJERCICIOS RESUELTOS EXPLICATIVOS

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

LÍMITES DE UNA FUNCIÓN - Límites laterales

Tema introductorio sobre el concepto de límite de una función de variable real se habla acerca de límites que no existen y límites cuyo resultado es infinito positivo o negativo.

De hecho se introduce el concepto de límites laterales y se expresa la necesidad de que tanto el límite por derecha y límite por izquierda de una función deben ser iguales para que el límite exista en ese punto.

En las clases anteriores veíamos ejemplos en donde se calculaba el límite de una función ya fuera utilizándola tabla de valores, la sustitución directa o el método grafico y veíamos que el limite existía, es decir siempre podíamos encontrar el límite de la función, en esta clase veremos ejemplos en donde no necesariamente existe el límite o donde se pueden llegar a límites que tienden al infinito.

Para esto supongamos que nos piden hallar el siguiente límite:

Si intentamos resolver este límite inicialmente utilizando la sustitución directa vemos que vamos a tener una división de 1/0 lo cual es una indeterminación. 

O si utilizamos la tabla de valores:

Podemos observar que al acercarnos al cero desde la izquierda la función crece vertiginosamente hacia abajo y si nos acercamos al cero por la derecha la fusión crece vertiginosamente hacia arriba,

En otras palabras, decimos que si nos acercamos al cero por la izquierda el límite tiende hacia menos infinito y si nos acercamos al cero desde la derecha el límite tiende hacia más infinito, por lo que decimos que el límite de esta función cuando x tiende a cero no existe. 

Podemos pensar de la siguiente manera: Si dividimos una cantidad  por un número muy pequeño el resultado del cociente será muy alto; por tal, cuando dividimos (1/x ) por cero, nos estamos acercando al infinito, dependerá si es por la izquierda de cero es infinito negativo y por la derecha de cero es infinito positivo.   Entonces este límite no existe.

A partir de este ejemplo podemos decir las siguientes generalidades, si tenemos un límite en el cual tenemos un número sobre cero (#/0) decimos que el límite no existe o es infinito positivo o infinito negativo.

 Pero si tenemos el caso (0/0)  decimos que probablemente exista el límite. Lo que debemos hacer es una manipulación algebraica para eliminar esta indeterminación y nos permita obtener :  

Otro ejemplo:

Cada vez que nos acercamos a cero, ya sea por la izquierda o derecha  la función crece positivamente infinito. 

mmmmmmmmmmmmmmmmmmmmmmmmmm

LÍMITE DE UNA FUNCIÓN - Formas de encontrar un límite

A través de un ejemplo como podemos encontrar el límite de la función mediante el uso de tres alternativas:

1. Evaluando la función en puntos cercanos al valor al cual tiende

2. Evaluando la función directamente en dicho valor

3. Haciendo uso de la gráfica de la función

A continuación hablamos acerca de límites y cómo calcularlos.

1. Evaluando la función en puntos cercanos al valor al cual tiende

Supongamos que si evaluamos la expresión con determinado número, y el resultado nos da 0/0, lo cual es indefinido.

Lo que hacemos es recurrir a la construcción de una tabla y ver qué empieza a suceder por derecha y por izquierda cuando nos acercamos al número que anula la expresión.

Utilizamos una calculadora para evaluar cada valor en la expresión, para ir sabiendo qué sucede con el límite. (En el ejemplo que vemos, cuando X tiende a uno por la izquierda o por la derecha, f(x) comienza a acerarse cada vez más a 2)

2. Evaluando la función directamente en dicho valor

Podemos también encontrar el límite mediante una “manipulación algebraica”.

Como en el ejemplo presentado, en el cual pudimos factorizar, y vemos que se cancela una parte de la expresión, y podemos simplemente evaluar el límite que nos piden en la ecuación.

3. Haciendo uso de la gráfica de la función.

Gráficamente también es posible resolver el límite, representando la función en el plano, y sabiendo que el número 1, que no se puede evaluar, constituye en la gráfica un punto que no tiene imagen en el plano, y que cada que nos acercamos a ese punto, nos acercamos al límite. Vemos que todas las imágenes se acercan  a dos (sin ser esta imagen de la función. 

En síntesis, presentamos tres formas de encontrar un límite: la primera es mediante el uso de tablas de valores; la segunda es tratar de eliminar el problema del cero sobre cero; la tercera es mediante el uso de la gráfica.

MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM

CÁLCULO DIFERENCIAL

MMMMMMMMMMMMMMMMMMMMM

1.- Límite – clase 1(Definición no formal de límite) 

2.- Límite - clase 2 (Formas de encontrar el límite de una función)

3.- Límite - clase 3 (Límites laterales)

4.- Límite - clase 4  (Propiedades de los límites)

5.- Límite - clase 5 (Solución de límites)

6.- Límite - clase 6 (Definición formal)


MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM


LÍMITE DE UNA FUNCIÓN

mmmmmmmmmmmmmmmmmmmmmmm<

A través de un ejemplo como podemos encontrar el límite de la función mediante el uso de tres alternativas:

1. Evaluando la función en puntos cercanos al valor al cual tiende

2. Evaluando la función directamente en dicho valor

3. Haciendo uso de la gráfica de la función

A continuación hablamos acerca de límites y cómo calcularlos.

1. Evaluando la función en puntos cercanos al valor al cual tiende

Supongamos que si evaluamos la expresión con determinado número, y el resultado nos da 0/0, lo cual es indefinido.

Lo que hacemos es recurrir a la construcción de una tabla y ver qué empieza a suceder por derecha y por izquierda cuando nos acercamos al número que anula la expresión.

Utilizamos una calculadora para evaluar cada valor en la expresión, para ir sabiendo qué sucede con el límite. (En el ejemplo que vemos, cuando X tiende a uno por la izquierda o por la derecha, f(x) comienza a acerarse cada vez más a 2)

2. Evaluando la función directamente en dicho valor

Podemos también encontrar el límite mediante una “manipulación algebraica”.

Como en el ejemplo presentado, en el cual pudimos factorizar, y vemos que se cancela una parte de la expresión, y podemos simplemente evaluar el límite que nos piden en la ecuación.

3. Haciendo uso de la gráfica de la función.

Gráficamente también es posible resolver el límite, representando la función en el plano, y sabiendo que el número 1, que no se puede evaluar, constituye en la gráfica un punto que no tiene imagen en el plano, y que cada que nos acercamos a ese punto, nos acercamos al límite. Vemos que todas las imágenes se acercan  a dos (sin ser esta imagen de la función. 

En, presentamos tres formas de encontrar un límite: la primera es mediante el uso de tablas de valores; la segunda es tratar de eliminar el problema del cero sobre cero; la tercera es mediante el uso de la gráfica.

MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM

SECCIÓN CÓNICA

MMMMMMMMMMMMMMMMMMM<

DEFINICIÓN DE SECCIÓN CÓNICA: El lugar geométrico de los puntos cuya relación de distancia a un punto y una recta fijos es constante recibe el nombre de sección cónica o simplemente cónica.

         

El punto fijo se llama foco de la cónica, (f).

          

La recta fija se llama directriz, (d).

          

La relación constante excentricidad, (e).

Las secciones cónicas se clasifican en tres categorías, según su forma y propiedades. Estas se establecen de acuerdo con los valores de La excentricidad.

Si e < 1, la cónica se llama elipse: 

      Si e = 1, la cónica se llama parábola:   

Si e > 1, la cónica se llama hipérbola

        

/span>

MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMI

Integral de una función par en seno y coseno

MMMMMMMMMMMMMMMMMMMMM

DEFINICIÓN DE SECCIÓN CÓNICA: El lugar geométrico de los puntos cuya relación de distancia a un punto y una recta fijos es constante recibe el nombre de sección cónica o simplemente cónica.

         

El punto fijo se llama foco de la cónica, (f).

          

La recta fija se llama directriz, (d).

          

La relación constante excentricidad, (e).

Las secciones cónicas se clasifican en tres categorías, según su forma y propiedades. Estas se establecen de acuerdo con los valores de La excentricidad.

Si e < 1, la cónica se llama elipse: 

      Si e = 1, la cónica se llama parábola:   

Si e > 1, la cónica se llama hipérbola

        

MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM

INTEGRAL DE UNA FUNCIÓN  IMPAR EN SENO

mmmmmmmmmmmmmmmmmmmmmmmm

http://www.tareasplus.com

Técnicas de integración: Método para integrar una función de seno y coseno que sea impar en la función seno

Para resolver este tipo de integrales se procede a hacer la sustitución t=cosx y luego encontrar el dx para la sustitución

Se muestran un par de ejemplo en este video

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

LA PARÁBOLA

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

Las parábolas aparecen en diferentes situaciones de la vida cotidiana. Se puede apreciar claramente cuando lanzamos un balón bombeado o golpeamos una pelota de tenis. En la curva que describe la pelota en su movimiento se puede ver que se trata de una trayectoria parabólica. Al dibujar este desplazamiento, podemos considerar esta parábola como la representación gráfica de una función que asigna a cada desplazamiento horizontal ‘x’ la altura ‘y’ alcanzada por la pelota.

Una vez situada la parábola en este marco, que es un sistema de coordenadas cartesianas, son visibles dos propiedades fundamentales: tiene un punto extremo, que corresponde al instante en el que la pelota alcanza la altura máxima. Este punto es el vértice de la parábola; y la segunda, en la que las alturas a las que llega la pelota son las mismas en posiciones horizontales equidistantes de la abcisa del vértice. Por tanto, la recta paralela al eje de ordenadas que pasa por el vértice es el eje de simetría de la parábola.

Name=1; HotwordStyle=BookDefault; Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.

La distancia entre el foco y la directriz de una parábola, recibe el nombre de parámetro de la parábola (suele denotarse por p).

Dada una parábola, se llama eje de simetría, la recta que contiene al foco y es perpendicular a la directriz.

Si la curva de la parábola, debe  cortar en el eje x en el punto cero.

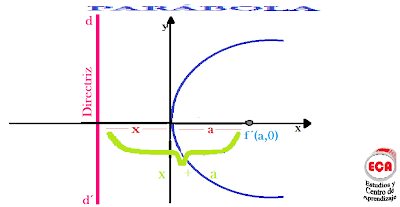
Sean d d´ la directriz y f el foco, la recta y el punto fijo. Tracemos por  
f (a,0), la perpendicular al eje x.

Sea      2 a     la distancia  de   f   a   DD´.

Por definición de parábola la curva debe cortar el eje x en el punto 0, equidistante de f y DD´. El eje y, se traza perpendicular al x por el punto 0. 

Las coordenadas de f son (a,0)

La ecuación de la directriz es: x + a = 0      o bien    
 x = - a.

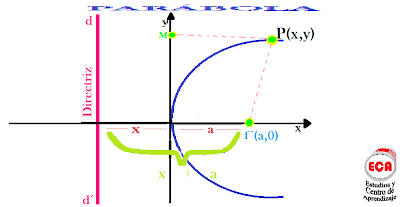
Sea P(x, y),  un punto genérico cualquiera.

Sea P(x,y) un punto genérico cualquiera de manera que

Entonces:

    

De la forma de la ecuación:                                                                            

, se deduce que la parábola es simétrica con respecto al eje x.

 El punto en que la curva corta el eje de simetría se denomina Vértice.

          

La cuerda CC´que pasa por el foco y es perpendicular  al eje se llama latus rectum.

          La longitud del latus rectum es 4a, es decir el coeficiente  del término de primer grado en la ecuación.

Si el foco está a la izquierda de la directriz, la ecuación toma la forma:

          Si el foco pertenece al eje y, la forma de la ecuación es: 

En la que el signo depende de que el foco esté  por encima o por debajo  de la directriz.

Consideremos ahora una parábola de vértice el punto P (h,k), de eje paralelo  al de coordenadas x y cuyo foco esté a una distancia  a del  vértice y a la derecha de él. La directriz. Paralela al eje y y a una distancia 2ª a la izquierda del foco, tendrá la  ecuación  x = h – a o bien, x – h + a = 0.

Llamaremos P(x, y) un punto genérico cualquiera de la parábola. Como PF = PM

Se llama vértice de la parábola al punto que corta su eje.

Para simplificar la parábola, se supondrá que el vértice es el origen de las coordenadas P (0,0) y que el foco (f), se encuentra en el semieje positivo de las abscisas.

FUNCION CUADRATICA.

Definición.

Una función cuadrática es aquella que puede escribirse de la forma: f(x) = ax² + bx + c, donde x es la variable independiente; y es la variable dependiente;  a, b y c coeficientes de la función y estos son números reales cualesquiera y a distinto de cero. Si representamos "todos" los puntos (x, f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.

La gráfica de la función cuadrática es una parábola y puede tener una de las siguientes seis posiciones.

Es decir, se puede abrir hacia arriba (figuras 1,2 y 3) o hacia abajo (figuras4, 5 y 6) y puede interceptar al eje x en dos puntos (figura 1 y 4), en un punto (figuras 2 y 5) o ningún punto (figuras 5 y 6)

A continuación se muestran tres funciones cuadráticas con sus respectivas gráficas, de tres funciones cuadráticas muy sencillas:

Para determinar el valor de las soluciones  X1 y X2 respectivamente es necesario utilizar la siguiente formula:

Los valores correspondientes a, a, b y c, los desprendemos de la ecuación general de la forma: a x² + bx + c = 0

 

La concavidad de la parábola

          O la posición en que se abre (hacia arriba o hacia abajo) está determinada por el signo del coeficiente de x²  

En la función y = a x² + bx + c, es decir, está determinada por el signo de “a”.

Así:

·       Si a > 0, entonces la concavidad es positiva y la parábola se abre hacia arriba.

·       Si  a < 0, entonces la concavidad es negativa y la parábola se abre hacia abajo.

Nota: “a” no puede tomar el valor cero, pues entonces la función sería lineal y no cuadrática.

 

Intersección de la parábola con los ejes.

 

a)-.Intersección con el eje Y: Como todos los puntos de este eje tienen la abscisa (eje x) x = 0, el punto de corte de la parábola con el eje Y tendrá de coordenadas (0, y).

     La intersección de la parábola con el eje y se obtiene haciendo

 x = 0 y corresponde por supuesto a y c.

     Todas las parábolas tienen un vértice, que corresponde al valor mínimo (si la parábola se abre hacia arriba). O el valor máximo (si se abre hacia abajo).

b)-. Intersección con el eje X: Como todos los puntos del eje X tienen la ordenada (eje y) y = 0, para ver estos puntos de corte se resuelve la ecuación de segundo grado ax² + bx + c = 0.

     Las intersecciones de la gráfica con el eje x, corresponden a las soluciones de la ecuación cuadrática asociada, es decir, a:

ax² + bx + c = 0 (Cuando y toma el valor de cero, la gráfica está sobre el eje x)

     Como sabemos, los tipos de soluciones de la ecuación dependen del signo del discriminante ∆ = b² - 4ac.

·       Si  ∆ = b² - 4ac → ∆ > 0, entonces las soluciones son reales y distintas y por lo tanto, hay 2 intersecciones con el eje x, éstas son los puntos X1 y X2.

·       Si  ∆ = b² - 4ac → ∆ = 0, entonces las soluciones son reales e iguales y por lo tanto, hay una sola intersección con el eje x, aquí X1  = X2.

·       Si  ∆ = b² - 4ac → ∆ < 0, entonces las soluciones son complejas conjugadas,  y por lo tanto, no hay una  intersección con el eje x.

Dependiendo del valor del discriminante (D) de la ecuación, se pueden presentar tres situaciones distintas:

A-.Si D > 0, la ecuación tiene dos soluciones reales sean X1 y X2  y estas sean distintas y la parábola cortará al eje X en dos puntos.

B-.Si D = 0, la ecuación tiene una solución real es decir X1 = X2  y, por tanto, la parábola cortará al eje X en un punto (que será el vértice).

C-.Si D < 0, la ecuación no tiene soluciones reales y la parábola no cortará al eje X. 

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

SECCIÓN CÓNICA

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

DEFINICIÓN : El lugar geométrico de los puntos cuya relación de distancia a un punto y una recta fijos es constante recibe el nombre de sección cónica o simplemente cónica.

          El punto fijo se llama foco de la cónica, (f).

          La recta fija se llama directriz, (d).

          La relación constante excentricidad, (e).

Las secciones cónicas se clasifican en tres categorías, según su forma y propiedades. Estas se establecen de acuerdo con los valores de La excentricidad.

        
Si e < 1, la cónica se llama elipse:      

          

 
Si e = 1, la cónica se llama parábola:   

 Si e > 1, la cónica se llama hipérbola. 

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

SECCIONES CÓNICAS

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm